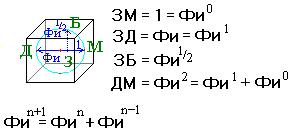"Геометрия «Вселенной движения»."
Окружающий нас мир представляет собой не вселенную материю, а вселенную движения.
Пространство и время являются взаимообусловленными аспектами движения, не существующие один без другого.
© Федор Пи «Геометрия «Вселенной движения».»
Постулаты теоретической системы Д. Ларсона.
Американский инженер Дьюи Б. Ларсон (Dewey B. Larson, 1898-1990) построил формализованную теоретическую систему «Вселенной движения», представленную им в трехтомнике «Структура физической вселенной» http://divinecosmos.e-puzzle.ru/list.php?c=larson_1 способную объяснить физические явления от субатомных частиц до скоплений галактик.
Его подход построения системы полностью формализован, не опирается на эмпирические данные, а основывается исключительно на следствиях из постулированных им свойств пространства и времени. Ларсон утверждает, что выведенная им из постулатов теоретическая модель вселенной пункт за пунктом соответствует наблюдаемой физической вселенной.
Теория Ларсона основывается на двух постулатах. Вот они:
Первый фундаментальный постулат: Физическая Вселенная целиком и полностью состоит из одного компонента – движения, существующего в трех измерениях, в дискретных единицах и с двумя взаимообусловленными аспектами – пространством и временем.
Второй фундаментальный постулат: Физическая вселенная описывается в терминах отношений обычной математики, ее первичные характеристики абсолютны, а геометрия евклидова.
В самой простой форме “уравнение движения”, выражающее это определение в математических символах, таково: v = s/t.
Оно говорит, что в движении пространство и время являются двумя взаимообратными аспектами этого движения и более ничем.
Самый простой способ определения статуса пространства и времени во Вселенной Движения – сказать, что пространство представлено числителем в выражении s/t, являющемся скоростью или быстродействием, измерением движения, а время, соответственно, знаменателем. Если нет дроби, нет ни числителя, ни знаменателя; если нет движения, нет ни пространства, ни времени. Пространство и время не существуют по отдельности; они существуют только в связи с движением.
Единица базового движения не обладает направлением; она является просто единицей пространства в связи с единицей времени. В количественных терминах это единица скалярной величины: единица скорости.
Векторное движение – это движение с неотъемлемым векторным направлением. Скалярное движение – это движение вовне или вовнутрь, не обладающее векторной направленностью, но с направлением приданном факторами, включающими связь направления с системой отсчета.
Ларсон постулирует мироздание составленное из дискретных единиц движения. Но это не значит, что движение происходит в виде ряда прыжков. Основное движение – это последовательность, в которой знакомая последовательность времени сопровождается аналогичной последовательностью пространства. Завершение одной единицы последовательности сразу же сопровождается возникновением другой, без перерыва.
Геометрическая модель постулируемой единицы движения.
Хотя Ларсон представляет варианты простых типов движения: вибрацию и гармоническое движение, он не предлагает геометрических образов этих движений, считая невозможным одновременное геометрическое представление движения и в пространстве и времени. По моему мнению это не верно. Базовым геометрическим образом единицы движения является круговое движение. Движение по окружности является балансом двух скалярных направленностей движения вовнутрь (гравитация) и вовне (инерция).
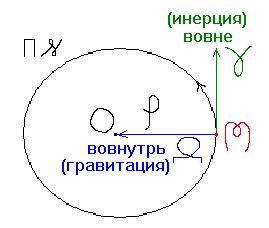
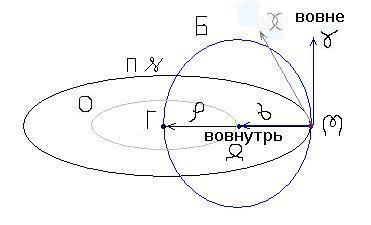
Схема единицы движения, состоящей из единицы пространства и единицы времени.
Один оборот кругового движения, взятый как целостность, обладает всеми свойствами обсуждаемыми Ларсоном: и единичностью, и непрерывностью, и скалярностью направлений участвующих сил: вовне и вовнутрь. Один оборот кругового движения является единой мерой и движения, и пространства, и времени, доли которых могут быть измерены на базе трансцендентного числа
p, являющегося пределом плоской геометрической фигуры имеющей максимальную площадь замкнутую непрерывной линией фиксированной (единичной) длины. Доли внутри единицы движения могут быть измерены как линейные проекции на две оси системы отсчета привязанной к началу единицы движения и смещенной в центральную точку.
Окружность, как геометрический образ единичного движения имеет несколько вложенных важных геометрических свойств-следствий, геометрические образы которых могут быть соотнесены со смысловыми знаками. Каждый из этих знаков будет иметь два аспекта: видимый – образ знака и скрытый – смысл, соотнесенный со знаком.
О – единица движения; круг;
Г – центр окружности; особенная внутренняя геометрическая точка присущая круговому движению;
Б – нечто вовне;
Р – радиус окружности; мерное свойство движения;
Д – скалярное направление движения вовнутрь;
У – скалярное направление движения вовне;
М – выделенная позиция на окружности, система отсчета движения (ДУМ);
П – проявленный, видимый аспект движения;
N(Н) – невидимый, информационный аспект движения;
Из этих букв-знаков можно составить слова русского языка, которые возможно интерпретировать геометрически. Например: дом, род, год, ум, мор, бог, дно, дурь, .
То что движение осуществляется в последовательности дискретных непрерывных единиц времени в одной или последовательности дискретных непрерывных единиц пространства согласуется с повседневным опытом и не вызывает возражений. Менее доступен пониманию разумом симметричный вариант движения в одной единице времени и череде непрерывных единиц пространства. Тем не менее аспекты движения пространство и время симметричны и все их свойства присущи обеим эти аспектам.
Для демонстрации движения в одной единице времени привожу пример. Возьмем единицу времени разделяемую фазой Луны, например, «Полнолуние». Планета Земля при своем движении в пространстве вокруг Солнца будет постоянно находится в этой единственной дискретной единице времени.
Геометрическая модель двумерного движения.
Д. Ларсон определяет двумерное движение формализованно, как отношение s²/t². Ларсон соотносит двумерное движение со свойствами магнетизма и электричества, но никакой геометрической интерпретации этого типа движения не предлагает.
Движение по окружности является геометрической моделью одномерного движения. Здесь характеристикой мерности движения служит радиус описываемой окружности траектории движения. Геометрической моделью двумерного движения является винтовой тор, пространственная форма которого содержит в себе одновременность двух круговых движений с различающимися радиусами. Из формализованного определения Ларсона никак не следует принципиальная разница мерностей двух движений участвующих в составном двумерном движении. При тождественности радиусов двух единичных движений их результирующее движение будет по прежнему круговым, т. е. одномерным.

В винтовом торе реализуется одновременность двух круговых движений: по кругу и радиусу тора.
В предыдущих моих работах «Модель полуцелого спина» и «Модель атома углерода» я рассказывал об уникальных геометрических свойствах орбиталей, движущихся вдоль стенок тора. О возможности геометрического совмещения несколькими орбиталями поверхности одного тора без их взаимопересечения. О парности орбиталей, имеющих полуцелое значение (1/2, 3/2, 5/2, …) отношения количеств оборотов кругового и радиального вращений.
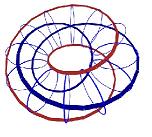

Парные орбитали на торе с полуцелым отношением количеств оборотов 1/2.
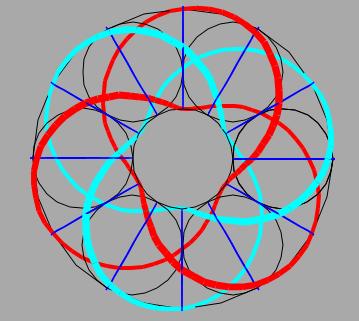
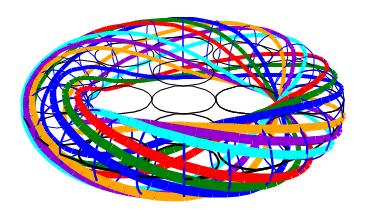
Орбитали с полуцелым отношением 3/2.
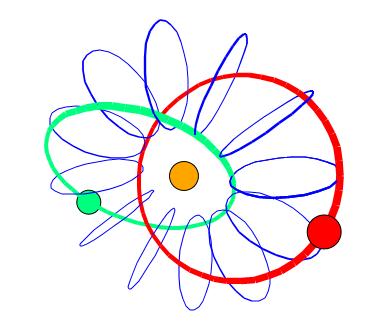
Парные орбитали на торе с отношением количеств оборотов кругового и радиального движений 1:1.
Тор является геометрической моделью единицы двумерного движения построенного из двух различающихся одномерных единиц движения. Невозможность материальными объектами совмещать пространство и время – это миф. Геометрически, например, нет препятствий совмещения несколькими двумерными движениями, являющимися орбиталями на поверхности тора, представляющего собой двумерную единицу движения, построенную на базе двух различающихся одномерных движений с взаимообусловленными аспектами пространства и времени.

Схема двумерной единицы движения, построенной из двух разных по мере одномерных единиц движения.
На рисунке-схеме двумерной единицы движения реализуется система отсчета ДУХ. В этом варианте направление «вовнутрь» у обеих одномерных единиц движения совпадают, а направления «вовне» ортогональны. Радиальный радиус тора (радиус вписанный) обозначен буквой Ять кириллицы, а радиальное направление «вовне» буквой Х. Буквой З отмечен центр витка радиального движения.
Двумерное движение геометрически представляет собой вложенность одного кругового движения некоторого радиуса в другое круговое движение большего радиуса. Траектория двумерного движение строится из конечных количеств витков. Геометрически количества круговых и радиальных витков в конкретных двумерных движениях могут быть разными. Разными относительно друг друга могут быть и значения описанного и вписанного радиусов.


Примеры двумерных движений с отношениями витков 1:5 и 12:1.
Тем не менее у всех двумерных движений имеются общие свойства, геометрические образы которых могут быть поименованы смысловыми знаками.
А – цепочка из дискретных единиц движения;
И – интерпретация последовательности единиц движения, как одна единичность;
С - структура; существование у движения более одной меры;
Т – текущая единица (одномерного) движения;
Л – предыдущая единица одномерного движения;
З – локализация одномерного движения в двумерном движении;
К – ограничение по направлению для двумерной единицы движения;
В – последовательный перебор элементов системы;
Из чего рождаются числа.
Смыслами букв-знаков К и Ч являются геометрические образы оснований чисел и чисел.
Из чего рождаются числа рассказано в книге Романова «Православная арифметика» http://www.skibr.ru/content/ass_Dub/img/sem/govorov/arifmet.pdf.
Числа рождаются из тора, то есть из структуры двумерной единицы движения, имеющей две различающиеся линейные меры – радиальный и круговой радиусы. Значения радиусов определяют систему исчисления чисел, основаниями которой являются два отрезка Меньший (М) и Больший (Д - дальний), на которые делится круговой диаметр тора радиальным радиусом.
Числами (Ч) являются вторые степени оснований чисел К. Ч = К * К. Основанием системы исчисления или по другому Целым числом называется сумма Меньшего числа и Большего числа. Ц = М * М + Д * Д. Для разъяснения рассмотрим разрез тора.
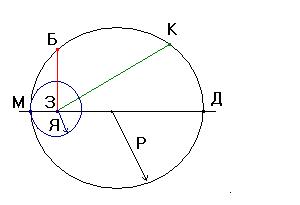
Схема расположения мерных отрезков Меньшего, Среднего и Большего
На рисунке буквами Р и Я обозначены круговой и радиальный радиусы тора. Круговой диаметр тора отрезок МД делится в точке З на два отрезка. Меньший отрезок МЗ, длина которого равняется радиальному радиусу, принимаемому за основание Меньшего числа единичной длины, и Больший отрезок ДЗ являющийся основанием Большего числа. Ортогональный отрезок БЗ является пропорционально Средним (Б – ближний) отрезком по отношению к Меньшему и Большему отрезкам. То есть длина отрезка МЗ относится к длине отрезка БЗ точно также, как длина отрезка БЗ относится к длине отрезка БЗ. Желающие могут проверить это свойство отрезков по теореме Пифагора.
И так, Меньшее : Среднее = Среднее : Большее
или Меньшее * Большее = Среднее * Среднее
Но Меньшее у нас по условию равняется единице, потому Большее есть вторая степень от Среднего. Но тогда по определению Числа - основание Большего числа равняется по величине Среднему числу. Д = Б * Б.
Точка К лежит на внешнем круге тора. Отрезок КЗ является основанием некоторого числа ЧЗ. Для геометрического построения числа по основанию числа следует увеличить масштаб тора, взяв в качестве новой единичной меры основание искомого числа. Все искомые числа будут по-прежнему лежать на лучах являющимися продолжениями отрезков оснований чисел. Точка М’ является пересечением окружности радиуса КЗ с центром в точке З и продолжения диаметра исходного тора МД. Величина отрезка М’З принимается в качестве новой единичной меры. Далее следует в такой же пропорции КЗ:МЗ увеличить круговой радиус тора Р’ = Р * (КЗ : МЗ). Пересечение этой окружности с продолжением луча КЗ даст искомую точку Ч. Длина отрезка ЧЗ будет в (КЗ : МЗ) * (КЗ : МЗ) раз больше по отношению к единичному отрезку МЗ, т. е. будет второй степень отрезка КЗ.
Следует построить отрезок M’Б’ параллельный отрезку МБ. Далее можно найти центр окружности Г’ радиуса Р’=Р*К, как точку пересечения ортогональной линии из середины отрезка М’Б’ и отрезка М’Д’ .
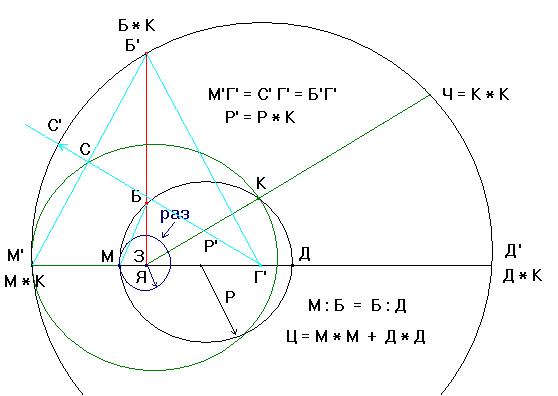
Схема построения полного числа Ч по основанию числа К
Выполнить такое построение для произвольных значений радиусов тора имея только «циркуль и линейку» затруднительно. Тем не менее имеются значения соотношений радиусов тора, при которых выполнить это построение просто. Имеется два простых варианта наборов чисел Меньшее, Среднее, Большее и Целое для которых все эти числа являются целочисленными величинами.
Пятеричная система исчисления.
При отношении радиального и кругового радиусов тора 1:1.5 имеем набор чисел: Меньшее = 1, Среднее = 2, Большее = 4 и Целое = 5.
Имея базовый единичный отрезок, зная отношение радиусов тора построить систему из четырех мерных отрезков имеющих относительные размеры √1, √2, √3, √4 и используя для этого только циркуль и линейку или с помощью веревочки и колышков, не представляет никакой сложности.
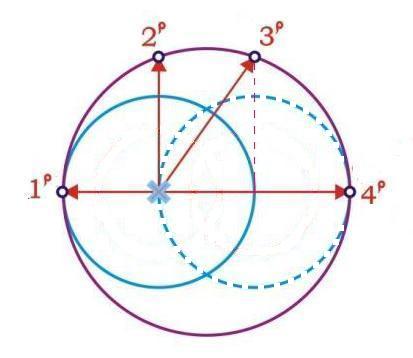
Схема расположения мерных отрезков пятеричной системы исчисления
Имея систему мерных отрезков оснований чисел можно, используя механизм построения полных чисел,
строить различные ряды мерных отрезков √2*√2, √2*√3, √2*√4, √2*√2*√2, √2*√2*√3, √2*√2*√4, ..., √3*√2, √3*√3, √3*√4, ...
Процесс умножения на Среднее, геометрически соответствует замещению мерных отрезков по кольцу и является механизмом роста всей конструкции. Т.е. Больший отрезок становится на место Среднего, Средний перемещается на место Меньшего. Новая длина Большего отрезка есть удвоенная длина нового Меньшего.
Новый радиус описанной окружности есть полусумма длин новых Меньшего и Большего отрезков. Вся конструкция при этом пропорционально увеличивается одновременно во всех своих частях на величину √2.
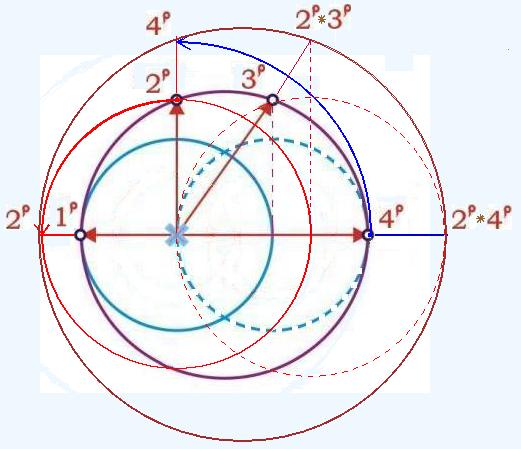
Механизм пропорционального роста системы одновременно во всех своих частях
Схема геометрического построения мерных отрезков оснований чисел пятеричной системы от 1 до 4 представляет собой геометрическую фигуру на плоскости. Совсем не сложно предложить аналогичную геометрическую схему построения оснований чисел пятеричной системы и в трехмерном Евклидовом пространстве. На рисунке ниже представлена такая пространственная схема.
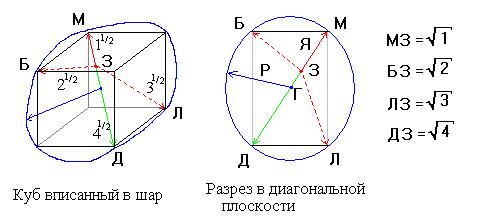
Пространственная схема пятеричной системы исчисления
Основой пространственной схемы является куб вписанный в шар. Диагональ куба, соединяющая противолежащие вершины куба МД делится в точке З на части в отношении 1:2. Длина отрезка МЗ принимается за единичную меру системы. Расстояния от точки З до вершин куба М, Б, Л, Д имеют мерные величины равные основаниям чисел пятеричной системы. Разрез куба и шара в плоскости вершин Б,М,Л,Д порождает исходную плоскую схему. Расстояния от точки З до других вершин куба имеют также мерные значения пятеричной системы, равные основаниям чисел 2 и/или 3.
Базовая точка системы З лежит не в центре системы, потому, вообще-то, основой пятеричной системы является совсем не шар, а тор с отношением радиусов радиального и кругового вращений 2:3. Вдоль стенок такого тора возможно проложить орбитали с полуцелыми значениями спинов 3/2, на трассы которых опереть вершины куба или вершины тетраэдров. На рисунках ниже представлены пространственные геометрические схемы для этого варианта.

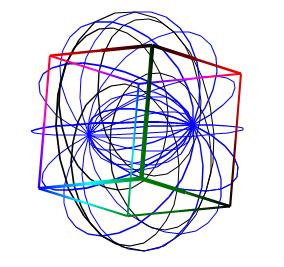

Базовой фигурой системы является тор
Пятеричная система исчисления закодирована в русской народной сказке «Курочка Ряба». Целое число 5 (яйцо) не соизмеримо с большим числом системы 4 (Дедка) и средним числом 2 (Бабка), но разбиваемо меньшим числом 1 (Мышка). Геометрическая форма двух перекрывающих наполовину одна другую окружностей представляет графику буквы «Веде» кириллицы.
Десятичная система исчисления.
При отношении радиального и кругового радиусов тора 1:2 имеем систему чисел: Меньшее = 1, Среднее = 3, Большее = 9 и Целое = 10. реализуется десятичная система исчисления.
1 : 3 = 3 : 9 и 1 + 9 = 10
Имея базовый единичный отрезок и зная отношение радиусов построить сразу всю систему девяти мерных отрезков чисел от 1 до 9 не представляет сложности. Сначала строятся основания чисел.
На рисунке ниже, вокруг двух примыкающих к другу полуокружностей единичного радиуса с центрами в точках А1 и А2 описана с центром в точке А3 полуокружность удвоенного радиуса. Из центров этих трех окружностей, а также серединных точек между центрами окружностей построены перпендикулярные отрезки до пересечения с описанной окружностью. Точки пересечения обозначены цифрами в степени ‘р’. Расстояния от центра вписанной окружности А1 до отмеченных точек на описанной окружности являются системой девяти мерных отрезков, вторые степени которых представляют собой отрезки с длинами кратными радиусу вписанной окружности от 1 до 9. Сомневающиеся могут проверить по теореме Пифагора справедливость этого утверждения.
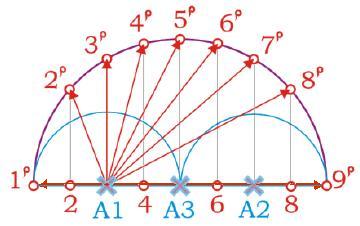
Схема расположения мерных отрезков десятичной системы исчисления
Меньшее число – радиус вписанной окружности, равное по величине единице именуется буквой Ять. Тогда Большее число выраженное по этой единичной мере будет именоваться Де в Ять или просто девять, а русское десять есть Де с Ять.
Персонажи в русской народной сказки «Репка» - дедка, бабка, внучка, жучка, мышка - являются закодированными числами десятичной системы исчисления.
Для десятичной системы также совсем не сложно предложить геометрическую схему построения оснований чисел в трехмерном Евклидовом пространстве. Основой для схемы по-прежнему являются шар и куб. Если для пятеричной системы шар описан вокруг куба и касается его вершин, то в варианте десятичной системы шар касается середин ребер куба. На рисунке ниже представлена такая пространственная схема.
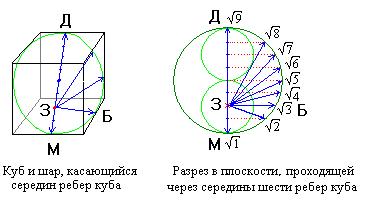
Пространственная схема десятеричной системы исчисления
Золотое сечение. Буква Ф.
Особенный случай двумерного движения представляет собой вариант при котором значения оснований чисел Меньшего, Среднего и Большего являются последовательными степенями некоторого особенного числа Ф. Такое число существует, и это известный математический факт.
И так, имеем по условию задачи: Меньшее М = Φⁿˉ¹, Среднее Б = Фⁿˉ½, Большее Д = Фⁿ, Целое Ц = М + Д или Фⁿ+¹ = Фⁿˉ¹ + Фⁿ.
При таком выборе соблюдается условие определения деления отрезка на две части в Золотом сечении. Больший отрезок так относится к Меньшему, как весь Целый отрезок к Большему. Д : М = Ц : Д = Ф.
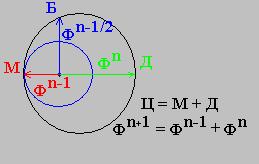
Схема расположения мерных отрезков системы базирующейся на числе Фи
Найдем следующие степени оснований этих чисел, умножив каждое на базовое число Ф¹/² = Б : М = Д : Б. Получим новые значения оснований чисел: Меньшее М = Фⁿˉ½, Среднее Б = Фⁿ, Большее Д = Фⁿ+½, Целое Ц = М + Д или Фⁿ+³/² = Фⁿˉ½ + Фⁿ+½.
Обратите внимание на движение значений по кольцу. Новое Меньшее стало предыдущим значением Среднего, а новое Среднее это предыдущее значение Большего. (В общем-то это справедливо и для пятеричной и десятичной системы.) Для полноты картины возможно дополнить схему еще одним основанием числа с наименованием Текущее (или Точка роста) Т и определить его начальное значение Т = Фⁿ+½.
В триаде Среднее, Большее, Текущее сохранится пропорция Ф¹/² = Д : Б = Т : Д, т.е Среднее играет роль Меньшего, Большее встает на место Среднего, а Текущее становится Большим. Имеем две пары мерных отрезков: М, Д и Б, Т, схожих по свойствам, но одновременно и различающихся.
ля Большего будет предыдущим значением Текущего, а новое значение для Текущего будет предыдущим значением для Целого.
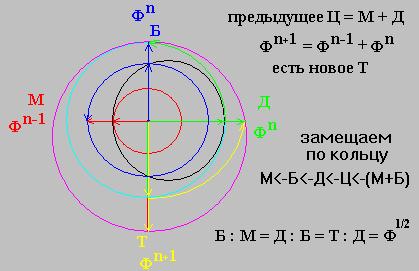
Механизм роста конструкции системы Фи на плоскости
Конечно, было бы горазда интереснее представить механизм одновременного пропорционального роста конструкции сразу во всех ее частях для трехмерного евклидова пространства, но на данный момент это не выполнено.
Для системы, основанной на золотом сечении, не сложно предложить геометрическую схему построения оснований чисел в трехмерном Евклидовом пространстве. Основой для схемы по-прежнему являются шар и куб. Если для пятеричной системы шар описан вокруг куба и касается его вершин, в варианте десятичной системы шар касается середин ребер куба, то в варианте системы Ф шар вписан в куб и касается середин граней куба. На рисунке ниже представлена такая пространственная схема.
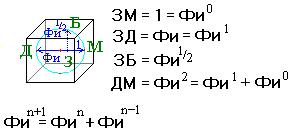
Пространственная схема системы основанной на золотом сечении
Для одного и того же куба реализуются три различные системы исчисления. Эти метрические системы используют три вложенные одна в другую сферические слоя-оболочки, проходящие через особенные точки куба: середины граней, середины ребер и углы.
Некоторые итоги.
И так, американский инженер Д. Ларсон высказывает мысль, что окружающий нас мир представляет собой не вселенную материи, а является вселенной движения.
Движение представляет собой единство двух взаимообусловленных аспектов: пространства и времени. Геометрической формой движения является окружность, радиус которой определяется как баланс двух скалярных направленностей движения: вовнутрь и наружу. Один оборот кругового движения является одной единицей движение, состоящий из одной единицы пространства и одной единицы времени. Единицы движения дискретны и непрерывны. По завершению одной единицы движения начинается следующая единица движения.
Окружность, как геометрический образ единичного движения имеет несколько важных геометрических свойств-следствий, геометрические образы которых могут быть соотнесены со смысловыми знаками. Каждый из этих знаков будет иметь два аспекта: видимый – образ знака и скрытый – смысл, соотнесенный со знаком-буквой. Например, смысл знака «О», является образ окружности, как единицы движения. Из букв-знаков можно складывать слова, которые также имеют за собой конкретные геометрические образы.
Следующим шагом является определение двумерного движения, как взаимосвязанность двух одномерных круговых движений с разными радиусами. Геометрическим образом такого движения является тор, имеющий круговое и радиальное вращения. Орбитали двумерных единиц движения проложены вдоль стенок тора. Тор может содержать в себе несколько орбиталей, т.е. единиц движения находящихся в одном пространстве и одном времени. Потому невозможность объектами совмещать время и пространство - это миф.
Центр окружности радиального вращения делит диаметр кругового вращения тора на две разновеликие части: Меньшую и Большую. На пропорциональности этих частей (Меньшее : Большее) строится система соизмеримостей частей конструкции. Особенный интерес имеют системы мерностей построенные на значениях пропорции 1:Фи, 1:2 и 1:3, соотносящиеся с «золотым сечением» и с пятеричной и десятичной системами исчисления.
В системе исчисления изначально заложен механизм одновременного пропорционального роста конструкции сразу во всех ее частях. Этот механизм реализуется через последовательное замещение текущих значений мерностей частей конструкции следующими значениями из системы мерностей.
Три простые системы мерностей могут быть совмещены на кубе в трехмерном Евклидовом пространстве. Куб имеет три сферических слоя-оболочки, проходящих через особенные точки куба: середины граней, середины ребер и углы. Диаметры этих сфер имеют пропорциональные мерности 1, √2 и √3 по отношению к ребру куба. На базе этих сфер и особенных точек куба и строятся системы исчисления из оснований чисел для систем «золотого сечения», пятеричной и десятичной.
Д. Ларсон считает, что элементарные частицы и атомы химических элементов являются конструкциями построенными из двумерных и одномерных единиц движения. Он предлагает конкретные варианты количеств единиц движения для всех атомов, но при этом не предлагает никакой геометрической интерпретации. Построение геометрических моделей атомов из базовых единиц движения может быть следующей задачей. Построение моделей для атомов водорода, углерода, азота и кислорода, являющихся основой биологической жизни, требуется, например, для исследования вопроса наличия для этих атомов общей системы соразмерностей.
* * *
Апрель 2014 г.
* * *